|
|
|
PC-ORD 7版最新更新
What's New |
New Graphs
|
- Hilltop Plot
-
A hilltop plot is a way of showing more than one nonlinear response surface at a time on a single graph. The first use that we are aware of was in Nelson et al. (2015). In PC-ORD, response surfaces are superimposed on an ordination as an overlay. This enables simultaneous measurement and display of one- and two-dimensional, non-linear community–trait–environment associations.
For each selected overlay variable, we trace a particular contour that is specified as a percentage of that variable's range. Each contained area is a "hilltop", and multiple partially transparent hilltops are superimposed on one ordination. The resulting diagram shows the maxima of many nonlinear overlay variables (e.g. traits, species abundances, or environmental variables) in a single figure.
Because the hilltops are based on a contoured response surface, you can better understand the basis for hilltop plots by reading about contour overlays. The chief difference in use between the hilltops and the contour plots is that contour plots can be shown for only one variable at a time, while one can graph many hilltops on the same ordination. This comes at a loss of information in that most of the contour plot is discarded when converting to a hilltop, but has the advantage of representing multiple nonlinear relationships at once..
- Contour Overlay
-
When you select a Q variable as an overlay, you are given a table of how the fit varies with the flexibility (smoothing parameter) used in the nonparametric regression of the overlay variable against the axis scores. If you choose "Optimize" flexibility, PC-ORDwill select the flexibility with the highest cross-validated fit (xR). If you wish to choose a specific value for flexibility, select "Specify" flexibility. Use the table presented under "Optimize" to help you choose a specific flexibility, if desired. Finally, you get a contour overlay onto the ordination space that you can customize to include color shading and/or contour interval labeling.
- Convex Hulls Filled Polygons
-
A convex hull is an overlay that uses a polygon to enclose all of the points in a group. The purpose of this overlay is to show the outline of a group by using the outermost points of that group in an ordination or a scatterplot. This can help the viewer to discern if and how groups are separated or overlap in the scatterplot.
The basic rule for forming the convex hulls is that the outer points in a group are connected in a closed polygon such that adjoining segments always make an interior angle less than or equal to 180 degrees. At least three points are needed to draw a convex hull. A convex hull for just three points must, however, have each of those points as a vertex (corner) of the polygon.
- NMS Stress by Iteration
A real-time display of how stress is changing with each iteration of NMS. The display is updated with every single step that attempts to improve the configuration of points in the ordination space.
This graph is meant to be both entertaining and informative. The entertainment is that you get a dynamic, colorful, interesting window into the progress of NMS. For every run and dimensionality you can see how stress is reduced as the iterations increase. Each dimensionality is color coded, and separate panels are displayed for the real and randomized runs.
Informativeness of these graphs comes from the insights into stability and consistency of alternative NMS solutions. Unstable configurations show up as vertical zig-zags. Consistency shows up as minimum stress plateaus at a given level. The importance of dimensionality shows up as a decreasing series of final stress as dimensionality increases.
|
|
Traits
PC-ORD 7 provides ways to relate data on species traits (trait matrix) to community samples (main matrix) and environmental data (second matrix). While many of these operations can be done in the other PC-ORD menu items, the Traits menu provides several operations specific to this kind of data.
|
- Functional Diversity
Functional diversity analyzes the combination of the sample unit x species matrix with a species x trait matrix. Functional diversity measures attempt to describe the diversity of species functional traits represented in a sample unit, rather that simply species diversity. For example, a plot containing three species, all having the same traits, are considered no more diverse than a single species. Similarly, two species with very different functional traits contribute more functional diversity than two species that are similar in their functional traits. For example, if we have two species in a plot and one is a weedy sun-loving pioneer plant species, and the other is a shade tolerant species with poor colonizing ability, that plot would have more functional diversity than two different species that were both shade tolerant poor colonizers.
- Fourth Corner Analysis
The methodological question of linking species traits to environmental variables, via the sample unit x species matrix, is called the fourth corner problem because of the arrangement of four basic matrices (see the traits x environment positions in Dray and Legendre (2008, Fig. 1a) and McCune and Grace (2002, Fig. 2.1). Fourth Corner Analysis provides statistical tests of the strength of the links between these matrices. For a detailed explanation of the theory and mathematics of fourth corner analysis see Legendre et al. (1997), Dray and Legendre (2008), Ter Braak et al, (2012), and Dray et al. (2014).
- Categorical to Binary
If, for a given variable, there are n unique categories (i.e., class levels with unique value labels), then n new binary (0/1) variables will be generated. Each new variable will be designated as a Q variable with value 0 or 1.
- Create Trait Combinations
Create one new categorical variable by combining categories from two existing variables. Each combination of categories from the two selected variables is taken as a new category in the new variable. The resulting new variable is always categorical. The existing variables are left intact, but you can easily remove them with Modify | Delete Columns.
For example, say you had two categorical variables, one coding for native vs. non-native species, and one coding for annuals vs. perennials. That might work well in the analyses, but what if species having a combinations of those, for example the non-native annuals, is particularly different ecologically from all remaining species You might, therefore, wish to create a new categorical variable with all four combinations of those trait categories: (1) native annuals, (2) native perennials, (3) non-native annuals, (4) non-native perennials.
- Calculate SU x Traits Matrix
Calculating a sample unit x trait matrix provides a flexible first step in analyzing the relationships between species traits and explanatory variables. This matrix is obtained by multiplying a sample unit x species matrix by a species x trait matrix, but the content of the resulting matrix depends on whether and how traits are standardized and whether or not the multiplication is followed by a weighted averaging step (McCune 2015). To maximize versatility of the SU x trait matrix, including comparability among traits, and usability with a wide range of distance measures, we recommend first standardizing traits by min-to-max, then calculating abundance-weighted trait averages in each sample unit.
- Species Distances in Trait Space
Species can be compared in their traits by calculating a distance matrix among species, starting with a species x trait matrix. Mathematically this is the same as calculating a distance matrix among sample units in species space, except that in this case the objects are species and their attributes are traits, rather than objects being sample units and the attributes species. The same distance measures are offered from the traits menu as for distances between sample units in species space.
|
|
New Matrix File Format
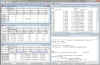 Interface Interface
|
- |
- Row and column indentifiers maximum length increased from 8 characters to
12 characters.
- Categorical values can now be either numerical (ShadeTolerQ in above example) or text (Dispersal, Leaf, Leaf, LearPersist, and ShadeTolerC in above example) with a maximum of
20 characters.
- Matrix size increased from 32,000 rows x 32,000 columns to
2,000,000 rows x 2,000,000 columns with a maximum of 536,848,900 elements with some limitations.
- Note: You can still import Excel old .wk1 files as well as .xls and .xlsx files.
|
|
|
New Analyses
|
- Fourth Corner Analysis
The methodological question of linking species traits to environmental variables, via the sample unit x species matrix, is called the fourth corner problem because of the arrangement of four basic matrices (see the traits x environment positions in Dray and Legendre (2008, Fig. 1a) and McCune and Grace (2002, Fig. 2.1). Fourth Corner Analysis provides statistical tests of the strength of the links between these matrices. For a detailed explanation of the theory and mathematics of fourth corner analysis see Legendre et al. (1997), Dray and Legendre (2008), Ter Braak et al, (2012), and Dray et al. (2014).
- Fuzzy Set (FSO)
Fuzzy set ordination applies fuzzy set theory to direct gradient analysis in ecological ordination. This ordination method requires the user to hypothesize the relationship between species communities and environmental variables or other predictors. The predictors are most commonly environmental variables, but they can also be a secondary set of species communities, or any other quantitative data set with the same number of rows as the community matrix. The community data are placed in the main matrix, and the secondary set is in the second matrix. The resulting ordination is an ordination of sample units in species space. Species can be superimposed on the ordination by a singleweighted averaging step
- Distance-based Redundancy Analysis (dbRDA)
Distance-based redundancy analysis (dbRDA) is similar to redundancy analysis (RDA), except that the main matrix is replaced by its principal coordinates, using a distance measure of your choice. The purpose of this variant is to allow you to choose non-Euclidean distance measures such as Sorensen (Bray-Curtis), that have proven effective in community ecology.
- Categorical Counts
Categorical Counts provides a way to track the number of cases (rows, usually sample units), with a given categorical value. By default this is done for all categorical variables in the selected matrix. This provides a quick assessment of the frequency of categories, which is useful for such issues as balance in experimental designs,or sampling effectiveness in different categories.
- Functional Diversity
Functional diversity analyzes the combination of the sample unit x species matrix with a species x trait matrix. The rationale and use of functional diversity measures in PC-ORD are described in the following topics.
|
|
Additions to Existing Analyses
|
- Gower Distance
Gower's (1971a) coefficient is highly unusual among measures of similarity or dissimilarity, because it can be calculated based on qualitative (categorical) data, quantitative data, or mixtures of the two. Categorical data are handled as a matching problem: items that share a qualitative attribute receive a unit of similarity from that attribute. See Legendre and Legendre (1998) for a detailed description of the method.
- Gower Distance, ignore 0,0
Gower (1971) and Legendre and Legendre (1998) suggested an intriguing but largely untested variant of Gower's coefficient of similarity that ignore 0,0 data pairs. If these double zeros are considered ambiguous information, you can exclude them from the computation of the coefficient. Sensitivity to double zeros is notorious in community ecology in producing unwanted effects on an analysis (Legendre & Legendre 1989, p. 253; McCune & Grace 2002, p. 38, 51).
Legendre and Legendre (1998) presented a modified version of the Gower coefficient of similarity (S19), calling it " asymmetrical" because matching zeros are handled differently than nonzeros. It is the same as the Gower coefficient, except that for quantitative variables (0,0) pairs are excluded and the sum of partial similarities is thus divided not by p variables, but by p* the number of non (0,0) pairs.
Note that this sense of "asymmetric" is different than in matrix symmetry. If Legendre's asymmetric version of Gower's similarity is converted to a distance (or dissimilarity) and used to build a distance matrix, this is still a symmetric matrix. In other words the distance between items A and B is the same as the distance between B and A, even if using the asymmetric version of Gower's similarity. To avoid that confusion PC-ORD uses the terminology "Gower, Ignore 0,0" in the menu system and output files.
- Morisita-Horn Distance
Horn (1966) modified Morisita's (1959) similarity measure, resulting in what is now known as Morista-Horn similarity or distance. The chief appeal of this distance measure is that it is relatively insensitive to sampling effort (Wolda 1981). It is thus most useful for cases where it is impossible to control the time, area, or volume of sampling.
The Morisita-Horn index is only weakly influenced by minor species, which is largely the reason that the method resistant to undersampling. At the same time, it makes the method insensitive to pattern that is carried in minor species.
- Increased maximum number of blocks or groups in perMANOVA and Indicator Species Analysis to 1000
- New Summary | Write distance matrix options:
|
在线留言
尊敬的客户朋友,如您有任何意见建议,请通过下表反馈给我们,我们会尽快与您联系。
|
|
|