正态性（和对数正态性）检验

Prism可以作为列统计分析的一部分来检验正态性。 作为非线性回归分析的一部分，它也可以检验来自非线性回归的残差的正态性。

如何：正态性检验

分析列数据

1.创建一个列数据表，以便每个数据集都在一个Y列中。

2.单击Analyze，查看Column analyses列表，然后选择正态性检验（Normality and Lognormality Tests）。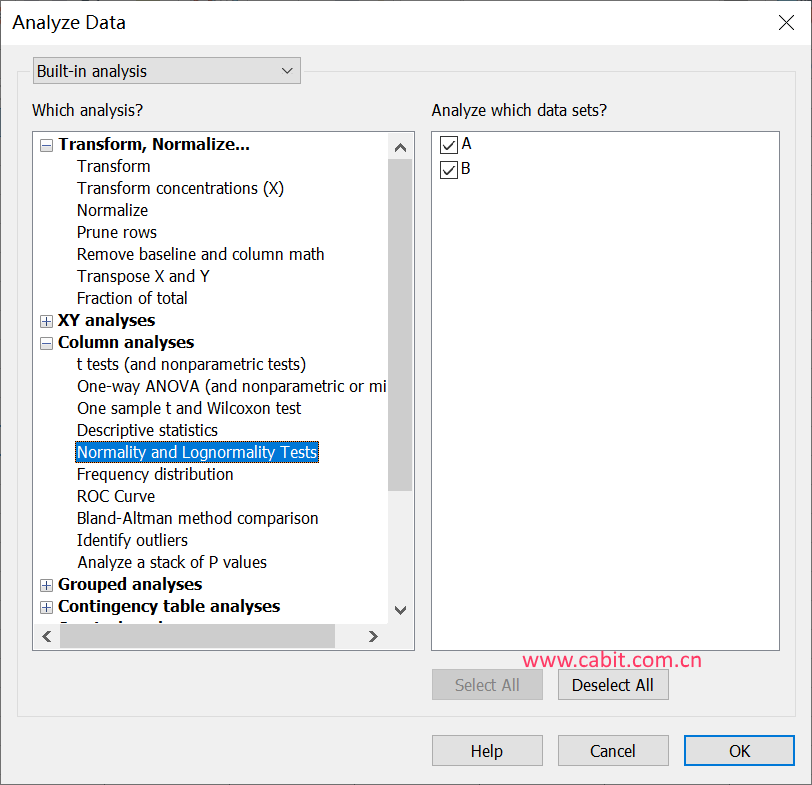

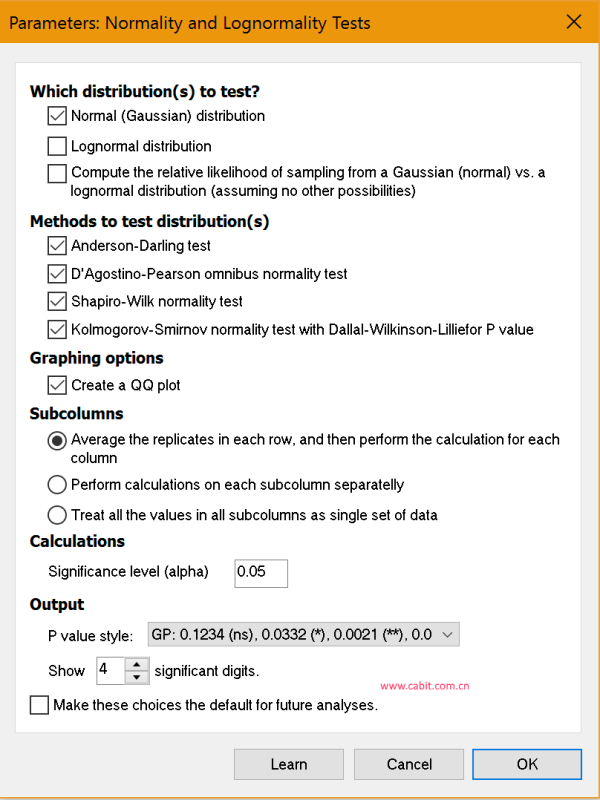3.Prism提供了四个检验正态性的选项。 选择这些选项中的一个或多个。 您也可以选择检验对数正态性并比较正态分布和对数正态分布。

选择一个正态性检验

Prism提供四个正态性检验。 为什么检验正态性的方法不只一种？ 分布可以有多种偏离高斯分布的方法，因此不同的正态性检验会得出不同的结果。

我们建议使用D'Agostino-Pearson正态性检验。 它首先计算偏度和峰度，以量化分布在不对称性和形状方面与高斯的距离。 然后，计算这些值与高斯分布的预期值相差多远，并从这些差异的总和中计算出一个P值。 这是一项功能强大的通用性检验，建议您使用。 请注意，D'Agostino开发了几种正态性检验。 Prism使用的一种是“综合K2”检验。

另一种方法是Anderson-Darling检验。 它通过将数据集的累积分布与高斯分布的理想累积分布进行比较来计算P值。 它考虑了累积分布曲线各部分的差异（与Kolmogorov-Smirnov检验不同，请参见下文）。

另一选择是Shapiro-Wilk正态性检验。 我们更喜欢D'Agostino-Pearson检验，原因有两个。 原因之一是，如果每个值都是唯一的，Shapiro-Wilk检验效果很好，但是当多个值相同时，它的效果就不好。 另一个原因是检验的基础很难理解。 有几种方法可以计算Shapiro-Wilk检验。 Prism使用Royston（1）的方法。

Prism的早期版本仅提供Kolmogorov-Smirnov检验。 我们仍然提供此检验（出于一致性考虑），但不再推荐。 它从一个值计算出一个P值：数据的累积分布与累积高斯分布之间的最大差异。 这不是一种评估正态性的非常敏感的方法，我们现在同意以下说法1：“ Kolmogorov-Smirnov检验只是历史上的好奇心，永远不要使用。” （2）。 请注意，此检验和Anderson-Darling检验都比较了实际和理想的累积分布。 区别在于，Anderson-Darling会考虑曲线所有部分的差异，而Kolmogorov-Smirnov只会考虑最大的差异。

最初发布的Kolmogorov-Smirnov方法假设您知道总人口的平均值和标准差（也许来自先前的工作）。 分析数据时，您几乎不了解总体平均值和标准差。 您只知道样本的平均值和标准差。 因此，为了计算P值，Prism使用Lilliefors方法（3）的Dallal和Wilkinson近似。 由于该方法仅适用于小P值，因此Prism对于大P值仅报告“ P> 0.10”。 万一遇到任何差异，您应该知道我们已经在多年前的Prism 4.01和4.0b中修复了该检验中的一个错误。

解释结果：正态性检验

正态性回答什么问题？

正态性检验均报告P值。 要了解P值，您需要了解原假设。 在这种情况下，零假设是所有值都是从遵循高斯分布的总体中采样的。

P值回答下面的问题：

如果该零假设成立，那么随机抽样数据与这些数据一样偏离理想高斯的机会是多少？

Prism还使用传统的0.05临界值来回答数据是否通过正态性检验的问题。 如果P值大于0.05，则答案为“是”。 如果P值小于或等于0.05，则答案为“否”。

如果正态性检验的P值高，我应该得出什么结论？

您只能说数据与高斯分布并不矛盾。 正态性检验不能证明数据是从高斯分布中采样的。 正态性检验所能做的就是证明与理想高斯的偏差不超过您仅凭偶然发现的偏差。 对于大型数据集，这令人放心。 对于较小的数据集，正态性检验没有足够的能力来检测与理想高斯值的适度偏差。

如果正态性检验的P值低，我应该得出什么结论？

零假设是从高斯分布中采样数据。 如果P值足够小，则您拒绝该原假设，并接受另一个假设，即该数据不是从高斯总体中采样的。 分布可能接近高斯分布（具有大数据集），也可能相距很远。 正态性检验不会告诉您关于替代分布的任何信息。

如果您的P值足够小，足以宣布与理想高斯的偏差为“统计上显著的”，那么您有四个选择：

• 数据可能来自另一个可识别的分布。 如果是这样，您可能可以转换您的值以创建高斯分布。 例如，如果数据来自对数正态分布，则将所有值转换为其对数。
• 一个或几个异常值的存在可能导致正态性检验失败。 运行离群值检验。 考虑排除异常值。
• 如果偏离正常值的幅度很小，则可以选择不执行任何操作。 对于轻度违反高斯假设的情况，统计检验往往非常可靠。
• 切换到非假设为高斯分布的非参数检验。 但是使用（或不使用）非参数检验的决定是一个重大决定。 它不应基于单个正态性检验，也不应自动化。

参考

1.P Royston, Remark AS R94: A Remark on Algorithm AS 181: The W-test for Normality. Journal of the Royal Statistical Society. Series C (Applied Statistics), Vol. 44, No. 4 (1995), pp. 547-551
2. RB D'Agostino, "Tests for Normal Distribution" in Goodness-Of-Fit Techniques edited by RB D'Agostino and MA Stephens, Macel Dekker, 1986.
3.Dallal GE and Wilkinson L (1986), "An Analytic Approximation to the Distribution of Lilliefors's Test Statistic for Normality," The American Statistician, 40, 294-296.

CALL or EMAIL 有关GraphPad Prism的更多信息，请联系我们的产品销售代表： 400-621-1085 021-50391087 或点击下面的图片，在线提交购买咨询信息 购买咨询